Project Work 5 - Canny Edge

Sebastian Dietz, Mischa Dombrowski

Overview

5: Canny-Edge

The Canny-Edge algorithm is one of the more advanced algorithms to perform edge detection. Unlike primitive approaches, like those you implemented in Task 4, Canny's algorithm leads to clearly defined edges (only one pixel in width) and a significant reduction in false detections (meaning regions of sharp brightness-transition, which are not edges of interest). This is achieved through the following process:

Blurring the image (Gaussian Blur) to reduce noise
Determining the image-gradient using the Sobel-kernel (→ Task 4)
Determining the gradient-direction for each pixel
Performing Non-Maximum-Suppression along the gradient-direction
Performing Hysteresis-Thresholding to select edges of intrest

These steps will be explained further later on.

5.1: Blurring and Gradient

The first part of this task can be implemented directly in the run-method of the Task_5_CannyEdgeDetection-class.

To do:

Convert the input-image to a FloatProcessor and apply a gaussian blur.

📝 Note:

The $\sigma$-parameter is one of the values you can play around with later on to improve your results. Once you are done, you will be able to set this value via a user-dialog. For now, a good starting point would be the value 2
Create 3 new FloatProcessors to store the image-gradient and the derivatives. Use the methods you implemented in Task 4 to apply a Sobel-operator and to calculate the gradient.

5.2 Determining Gradient-Directions

To calculate the direction of each pixel, you will now implement a new method called getDir. The formula for calculating the gradient-direction at a given pixel is:

Θ = atan2(G_y , G_x)

with G_y and G_x being the values of the respective y- and x-derivatives at the current position.

📝 Note:

The gradient-direction provides information about the angle or direction of an edge within the image. At any given point the edge will be perpendicular to the gradient direction. This will become important when it comes to performing Non-Maximum-Suppression (NMS). An example:

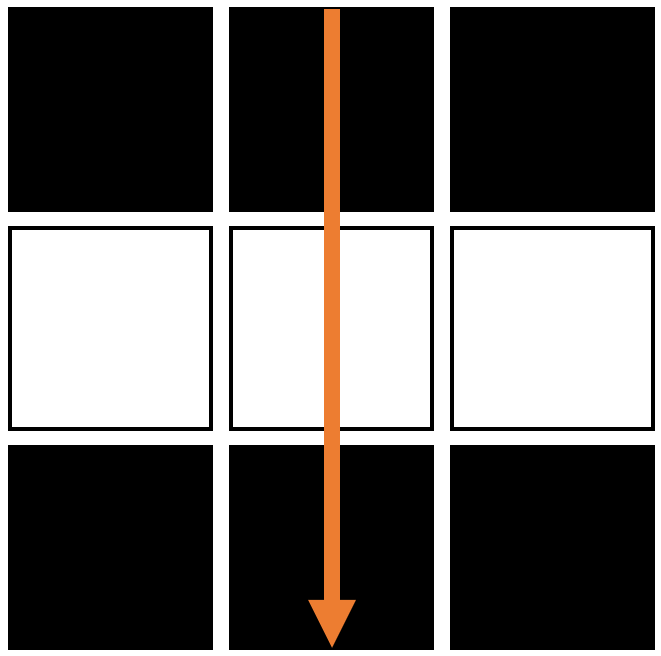
white pixels ≙ edge; arrow ≙ gradient-direction

The atan2-method used to determine the direction returns the angle $\Theta$, that results from converting a cartesian coordinate (x,y) to radians (r,$\Theta$). The angle theta is therefore returned in radians and you will need to convert it to degrees.

⚠ Important warning: ⚠
The atan2-method expects coordinates in a standard cartesian coordinate-system (x→ / y↑). Since you are working with images, the y-axis is defined differently (x→ / y↓) and you will therefore need to call the method like this: Math.atan2 (-y, x)

The getDir-method will determine the gradient-direction for each pixel and then round it to one of the following values: 0°, 45°, 90°, 135°. These stem from the fact that an image is a discrete set of pixels and therefore we can only differentiate between these directions.

Gradient-directions: 0°, 45°, 90°, 135°

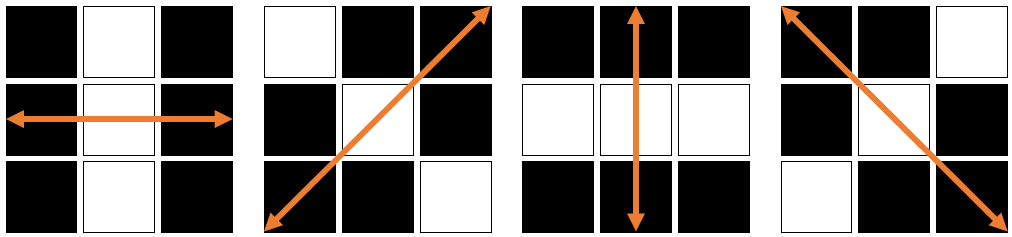
To do:

Create a new method:

public ByteProcessor getDir (FloatProcessor X_Deriv, FloatProcessor Y_Deriv){}

Create a ByteProcessor to store the directions
Create an int-array:
```
int[] angles = {0,45,90,135,180};
```
(180° is equivalent to 0° but needs to be considered as a seperate case)
Iterate through the input-FloatProcessors and calculate the direction for each pixel (in degrees). Remember that the y-axis is inverted.
Search for the closest match in the angles-array and store the final direction in the output-ByteProcessor.

📝 Note:
Negative values are simply "mapped" to the corresponding positive value (for example -45° ≙ 135° or -90° ≙ 90°). You can do this by simply checking if the value is negative and then adding 180°. If the closest match is 180° the direction is set to 0°
Return the final ByteProcessor

5.3: Non-Maximum-Suppression

During NMS the goal is to reduce edges to a single-pixel-line. This is achieved by searching for local intensity-maxima in the Gradient-Direction, so that edge-information is preserved, but the blurriness of primitive edge-detection tools is removed.

More specifically, this works by checking each pixel in relation to its two neighbouring pixels (along the gradient-direction). If the pixel is the highest of the three, it is kept as part of the edge. If not, it is discarded (set to 0).

To do:

Create a new method:

public FloatProcessor nonMaxSuppress(FloatProcessor Grad, ByteProcessor Dir) {}

Create a new FloatProcessor to store the resulting image
Iterate through the gradient-image. Check the direction for each pixel and then evaluate whether or not it is a local maximum in gradient-direction.
If it is a local maximum, store the value in the output-FloatProcessor
Return the final FloatProcessor

5.4: Hysteresis Thresholding

Hysteresis Thresholding is a special form of thresholding, which uses two threshold-values instead of one (upper and lower). Similar to standard thresholding, if a pixel's value falls above the upper threshold, it is kept as part of the image. If however, the pixel's value falls below, or is equal to the upper threshold, but above the lower threshold, the pixel is only kept as part of the image, if it is directly connected to a pixel above the upper threshold. Any pixel equal to or below the lower threshold is disregarded.

To do:

Create a new method:

public ByteProcessor hysteresisThreshold (FloatProcessor In, int upper, int lower){}

Since you are working with a FloatProcessor and the values a pixel can have are not the easiest to work with, you can instead convert your input-values to percentages of the maximum value within the image. To do so, simply add:
```
float tHigh = ((float)In.getMax()*upper)/100f;
float tLow = ((float)In.getMax()*lower)/100f;
```
You can then use tHigh and tLow as your threshold values, while being able to define them through low integer numbers. As a starting point you can for example use 15 as upper and 5 as lower. Feel free to experiment around with these.
Create an output-ByteProcessor to store the final image
Iterate through the input image and check the threshold condition for each pixel. Set pixels above the upper limit to white in the output image
In order to check, whether a pixel above the lower threshold is connected to an existing edge, you will need to iterate through the image again and check the connections repeatedly, because a pixel can become connected to the edge through any number of adjacent pixels. To avoid mistakes here, the following code, as well as the included hasNeighbours()-method will be provided. You can simply add this code after you performed the first iteration through the image.
```
boolean changed = true;
while (changed) {
   changed = false;
      for (int x = 0; x < In.getWidth(); x++) {
         for (int y = 0; y < In.getHeight(); y++) {
            if (In.getPixelValue(x, y) > tLow && hasNeighbours(Out, x, y) && Out.getPixel(x,y)==0) {
                     Out.set(x, y, 255);
                     changed = true;
                 }
             }
         }
     }
```
(Out refers to the output-image. If you named it differently, you can obviously change the code accordingly)
Return the output image

Add a simple user-dialog to the run-method, which allows you to select values for $\sigma$, the upper threshold and the lower threshold.

Finally perform the getDir,nonMaxSuppress and hysteresisThreshold steps in sequence within your run-method and display your final result.

5.5: Project-Report

The part of your report concerning Task_5 should contain the following:

A short description of what Canny-Edge-Detection aims to do and how it works
In which ways it is superior to the more primitive approaches
Images you generated with your code. How do the parameters influence your results?